일반 상대성이론] 우주론 (cosmology); 우주의 미래와 가속 팽창

Einstein Gravitational Field Equation

$R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R=\frac{8\pi G}{c^4}T_{\mu \nu }-\Lambda g_{\mu \nu }$Rμν​−12​gμν​R=8πGc4​Tμν​−Λgμν​​

$R_{\mu \nu }:\ \text{Rcci curvature tensor}$Rμν​: Rcci curvature tensor​

$R:\ \text{Scalar Curvature}$R: Scalar Curvature​

$T_{\mu \nu }:\ \text{Energy-momentum Tensor}$Tμν​: Energy-momentum Tensor​

$\Lambda :\ \text{Comological Constant}$Λ: Comological Constant​

아인슈타인 중력장 방정식(Einstein Gravitational Field Equation)은 에너지와 질량이 시공간에 얼마만큼 있으면, 공간이 어떻게 휘게 되는지 알려주는 방정식이다. 각 항의 의미는 아래에 적었다. 텐서 곡률인 리치 곡률 텐서(Ricci curvature tensor)와 스칼라 곡률(scalar curvature) R이 휘어진 공간에 대한 정보를 준다. 사이에 있는 gμν는 메트릭텐서로 전체 식의 형태를 텐서로 맞추기 위해 있다. 에너지-모멘텀 텐서(energy-momentum tensor) Tμν는 시공간의 에너지와 질량의 정보를 담고 있다. 특히 T00은 에너지에 대한 정보를 담고 있다. Tμν가 담고 있는 정보는 아래와 같다고 한다.

출처: 위키피디아

우주상수(cosmological constant) Λ는 우주가 팽창하는 것을 막기 위해서 아인슈타인(Einstein)이 임의로 추가한 값이다. 스칼라 곡률 R과 동일하게 텐서 형태를 위해 메트릭 텐서가 곱해져 있다.

종합하면 위 방정식은 공간에 에너지와 질량이 어떻게 있는지 알려주면, 시공간이 어떻게 휘어지는지 알려주는 식이다.

Curvature

아인슈타인은 3차원 곡률(Curvature)에 대한 정보 포함한다. 그에 앞서 2차원 곡률을 알아보자.

​

- 가우스 곡률(Gaussian Curvature)

2차원에서 곡률은 가우스 곡률(Gaussain curvature)라는 개념을 적용해서 나타낸다. 이는 다음과 같다.

$k\equiv \frac{\ A_2}{A_1}\ \left[\text{Gaussian Curvature}\right]$k≡ A2​A1​​ [Gaussian Curvature]​

$A_1:\text{Area that unit vectors move}$A1​:Area that unit vectors move​

$A_2:\ \text{Area that unit vectors sweep on unit sphere}$A2​: Area that unit vectors sweep on unit sphere​

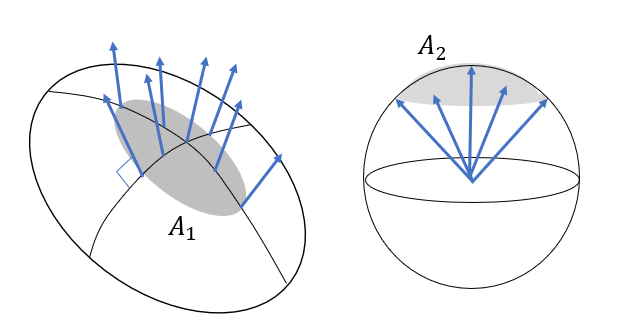
가우시안 곡률에서 다음 둘은 같은 곡률이 "0"으로 같다.

A4 용지를 양쪽에서 밀어서 휘어진 것 같은 공간과 평면은 A2가 0이라서 가우시안 곡률이 "0"으로 동일하다.

​

- 리만 곡률 (Riemann Curvature)

3차원에 대한 곡률 개념이 리만 곡률이다. (사실 강의에서는 자세한 설명이 없었다.) 이는 다음과 같이 정의한다.

$\left(\partial _{\alpha }\partial _{\beta }-\partial _{\beta }\partial _{\alpha }\right)e_r\equiv R_{\alpha \beta \gamma }^{\delta }e_{\delta }$(∂α​∂β​−∂β​∂α​)er​≡Rδαβγ​eδ​​

$R_{\alpha \beta \gamma \delta }=g_{\alpha \epsilon }R_{\beta \gamma \delta }^{\epsilon }\ \left[\text{Rimman Curvature Tensor}\right]$Rαβγδ​=gαε​Rεβγδ​ [Rimman Curvature Tensor]​

물리학에서 흔히 다른 변수에 대해 두 번 미분한 경우는 서로 순서를 바꿔도 무관하다. 그러나 일반적으로는 그렇지 않다. 그때 발생하는 차이를 리만 곡률(Riemann Curvature)이라고 한다.

리만 곡률에 대해서 한번 contraction한 것이 리치 곡률 텐서이고, 여기서 한번 더 contraction 한 것이 스칼라 곡률이다.

$R_{\alpha \beta \gamma \delta }=g_{\alpha \epsilon }R_{\beta \gamma \delta }^{\epsilon }\ \left[\text{Rimman Curvature Tensor}\right]$Rαβγδ​=gαε​Rεβγδ​ [Rimman Curvature Tensor]​

$R_{\alpha \beta }=R^{\beta }\alpha \beta \gamma =g^{\beta \nu }R_{\nu \alpha \beta \gamma }\ \left[\text{Ricci Curvautre Tensor}\right]$Rαβ​=Rβαβγ=gβνRναβγ​ [Ricci Curvautre Tensor]​

$R=R_{\alpha }^{\alpha }=g^{\alpha \beta }R_{\alpha \beta }\ \left[\text{Scalr Tensor}\right]$R=Rαα​=gαβRαβ​ [Scalr Tensor]​

Friedman-Lemaitre-Robertson-Walker Metric

시간이 지나도 물질의 분포가 변하지 않는다고 가정하고 아인슈타인 중력장 방정식을 풀면 프리드만-레메트르-로버트슨-워커 계량(Friedman-Lemaitre-Robertson-Walker Metric)가 나온다.

$ds^2=c^2dt^2-R\left(t\right)^2\left\{\frac{dr^2}{1-kr^2}+r^2d\Omega ^2\right\}\ \left[\text{Friedman-Lemaitre-Robertson-Walker Metric}\right]$ds2=c2dt2−R(t)2{dr21−kr2​+r2dΩ2} [Friedman-Lemaitre-Robertson-Walker Metric]​

여기서 R이 일정하고 k=1인 경우는 3차원 구 표면에서의 좌표계를 나타낸다.

$ds^2=R^2\left(\frac{dr^2}{1-r^2}+r^2d\Omega ^2\right),\ r\equiv \frac{r"}{R}\ \left[\text{3D Sphere surface Coordinate}\right]$ds2=R2(dr21−r2​+r2dΩ2), r≡r′R​ [3D Sphere surface Coordinate]​

생각을 쉽게 하기 위해서 2차원 구 표면에서 생각하자.

$x^2+y^2+z^2=R^2$x2+y2+z2=R2​

$Let\ \ r"^2=x^2+y^2,\ \theta =\tan \left(\frac{y}{x}\right).\ Then,$Let r′2=x2+y2, θ=tan(yx​). Then,​

$r"^2+z^2=R^2$r′2+z2=R2​

$z^2=R^2-r"^2$z2=R2−r′2​

$zdz=-r"dr"$zdz=−r′dr′​

$dx^2+dy^2=dr"^2+r"^2d\theta ^2$dx2+dy2=dr′2+r′2dθ2​

$$​

$ds_{on\ s^2}^2=\left[dx^2+dy^2+dz^2\right]_{on\ s^2}=\left[dr"^2+r"^2d\theta ^2+dz^2\right]_{on\ s^2}$ds2on s2​=[dx2+dy2+dz2]on s2​=[dr′2+r′2dθ2+dz2]on s2​​

$=\left[dr"^2+r"^2d\theta ^2+\frac{r"^2}{z^2}dr"^2\right]=\left(1+\frac{r"^2}{z^2}\right)dr"^2+r"^2d\theta ^2$=[dr′2+r′2dθ2+r′2z2​dr′2]=(1+r′2z2​)dr′2+r′2dθ2​

$=\left(1+\frac{r"^2}{R^2-r"^2}\right)dr"^2+r"^2d\theta ^2=\frac{R^2}{R^2-r"^2}dr"^2+r"^2d\theta ^2$=(1+r′2R2−r′2​)dr′2+r′2dθ2=R2R2−r′2​dr′2+r′2dθ2​

$Let\ r=\frac{r"}{R},\ dr=\frac{dr"}{R}.\ Then,$Let r=r′R​, dr=dr′R​. Then,​

$ds_{on\ s^2}^2=R^2\left[\frac{\frac{1}{R^2}dr"^2}{1-\frac{r"^2}{R^2}}+\frac{r"^2}{R^2}d\theta ^2\right]=R^2\left[\frac{dr^2}{1-r^2}+r^2d\theta ^2\right]$ds2on s2​=R2[1R2​dr′21−r′2R2​​+r′2R2​dθ2]=R2[dr21−r2​+r2dθ2]​

$ds_{on\ s^3}^2=R^2\left[\frac{dr^2}{1-r^2}+r^2\left(d\theta ^2+\sin ^2\theta d\phi ^2\right)\right]$ds2on s3​=R2[dr21−r2​+r2(dθ2+sin2θd?2)]​

여기서 R이 일정하고, k=-1인 경우는 2차원 쌍곡면에서의 좌표계가 된다.

$ds_{on\ H^3}^2=R^2\left(\frac{dr^2}{1-r^2}+r^2d\Omega ^2\right),\ r\equiv \frac{r"}{R}\ \left[\text{3D hyperbola surface Coordinate}\right]$ds2on H3​=R2(dr21−r2​+r2dΩ2), r≡r′R​ [3D hyperbola surface Coordinate]​

이것도 위와 유사한 방식으로 유도할 수 있다.

$x^2+y^2-z^2=-R^2$x2+y2−z2=−R2​

$r"^2=x^2+y^2,\ \theta =\tan \left(\frac{y}{x}\right)$r′2=x2+y2, θ=tan(yx​)​

$z^2=r"^2+R^2\to zdz=r"dr"$z2=r′2+R2→zdz=r′dr′​

$ds_{on\ H^2}^2=\left[dx^2+dy^2-dz^2\right]_{on\ H^2}=\left[dr"^2+r"^2d\theta ^2-\frac{r"^2}{z^2}dr"^2\right]$ds2on H2​=[dx2+dy2−dz2]on H2​=[dr′2+r′2dθ2−r′2z2​dr′2]​

$=\left(1-\frac{r"^2}{z^2}\right)dr"^2+r"^2d\theta =\left(1-\frac{r"^2}{r"^2+R^2}\right)dr"^2+r"^2d\theta $=(1−r′2z2​)dr′2+r′2dθ=(1−r′2r′2+R2​)dr′2+r′2dθ​

$=\left(\frac{R^2}{r"^2+R^2}\right)dr"^2+r"^2d\theta =R^2\left[\frac{\frac{1}{R^2}dr"^2}{1+\frac{r"^2}{R^2}}+\frac{r"^2}{R^2}d\theta ^2\right]=R^2\left[\frac{dr^2}{1+r^2}+r^2d\theta ^2\right]$=(R2r′2+R2​)dr′2+r′2dθ=R2[1R2​dr′21+r′2R2​​+r′2R2​dθ2]=R2[dr21+r2​+r2dθ2]​

$\therefore ds_{on\ H^2}^2=R^2\left[\frac{dr^2}{1+r^2}+r^2d\theta ^2\right]$∴ds2on H2​=R2[dr21+r2​+r2dθ2]​

$ds_{on\ H^3}^2=R^2\left[\frac{dr^2}{1+r^2}+r^2\left(d\theta ^2+\sin ^2\theta d\phi ^2\right)\right]$ds2on H3​=R2[dr21+r2​+r2(dθ2+sin2θd?2)]​

또한 R이 일정하고 k=0인 경우는 평면을 나타낸다.

$ds^2=R^2\left[dr^2+r^2\left(d\theta ^2+\sin ^2\theta d\phi ^2\right)\right]\ \ \left[\text{Euclidean space}\right]$ds2=R2[dr2+r2(dθ2+sin2θd?2)] [Euclidean space]​

가우시안 곡률 k에 별로 R이 일정할 때, 프리드만-레메트르-로버트슨-워커 계량은 3 가지 공간을 나타낸다.

k=0 ⇒ Euclidean space

k=1 ⇒ 3D sphere surface space

k=-1 ⇒3D hyperbola surface space

​

Friedman Equation; Future of Universe

아인슈타인 중력장 방정식에 허블 법칙을 적용하면 우리 우주의 미래를 점쳐볼 수 있다. 여기서 허블 법칙은 다음과 같이 적을 수 있다.

$H\left(t\right)=\frac{\dot{R}\left(t\right)}{R\left(t\right)}\ \left[\text{Hubble Law}\right]\ \ \text{cf)}\ \ v=H\cdot d$H(t)= ˙R (t)R(t)​ [Hubble Law] cf) v=H·d​

시간에 대한 (μ=0, ν=0인 경우) 아인슈타인 중력장 방정식으로부터 프리드만 방정식(Friedmann euqation)을 유도할 수 있다.

$R_{00}-\frac{1}{2}g_{00}R=\frac{8\pi G}{c^4}T_{00}-\Lambda g_{00}$R00​−12​g00​R=8πGc4​T00​−Λg00​​

$\to H^2=\frac{8\pi G\rho }{3}+\frac{1}{3}c^2\Lambda -c^2\ \frac{k}{R^2}\ \left[\text{Friedmann equation}\right]$→H2=8πGρ3​+13​c2Λ−c2 kR2​ [Friedmann equation]​

(중력방정식에서 그 다음식이 나오는 과정은 자세한 풀이는 본 강의에서 나오지 않았다.)

이제 프리드만 방정식을 살짝 수정하면 우주의 미래에 대해 점쳐볼 수 있다.

$1=\frac{\rho }{\frac{3H^2}{8\pi G}}+\frac{c^2\Lambda }{3H}-\frac{c^2k}{H^2R^2}$1=ρ3H28πG​​+c2Λ3H​−c2kH2R2​​

$\frac{c^2k^2}{H^2R^2}=\frac{\rho }{\rho _c}+\frac{c^2\Lambda }{3H}-1\left(\because \rho _c\equiv \frac{3H^2}{8\pi G}\right)$c2k2H2R2​=ρρc​​+c2Λ3H​−1(∵ρc​≡3H28πG​)​

$=\ \Omega _m+\Omega _{\Lambda }-1\left(\because \Omega _m\equiv \frac{\rho }{\rho _c},\ \Omega _{\Lambda }\equiv \frac{c^2\Lambda }{3H}\right)$= Ωm​+ΩΛ​−1(∵Ωm​≡ρρc​​, ΩΛ​≡c2Λ3H​)​

$When\ \Omega _{\Lambda }=0,\ then$When ΩΛ​=0, then​

$\frac{c^2k^2}{H^2R^2}=\ \Omega _m-1$c2k2H2R2​= Ωm​−1​

우주상수의 효과가 없다고 가정하면, Ωm 에 따라 총 3가지의 미래가 점쳐진다.

$\Omega _m\equiv \frac{\rho }{\rho _c}=1\to \frac{c^2k^2}{H^2R^2}=0\to k=0\ \to 크기가\ 일정한\ 우주$Ωm​≡ρρc​​=1→c2k2H2R2​=0→k=0 →크기가 일정한 우주​

$\Omega _m\equiv \frac{\rho }{\rho _c}>1\to \frac{c^2k^2}{H^2R^2}>0\to k>0\to 구형태의\ 우주.\ \left(팽창\ 후\ 수축하는\ 우주\right)$Ωm​≡ρρc​​>1→c2k2H2R2​>0→k>0→구형태의 우주. (팽창 후 수축하는 우주)​

$$​

$\Omega _m\equiv \frac{\rho }{\rho _c}<1\to \frac{c^2k^2}{H^2R^2}<0\to k<0\to 쌍곡형태의\ 우주.\ \left(계속\ 팽창\right)$Ωm​≡ρρc​​<1→c2k2H2R2​<0→k<0→쌍곡형태의 우주. (계속 팽창)​

​

즉, 임계밀도 ρc를 넘지는 지 여부가 우주의 미래를 점치는데 가장 중요한 요소이다. 교양적으로 보면 물질이 많으면 서로 잡아당겨서 수축하는 우주가 되고, 적당히 있으면 팽창하는 힘과 수축하는 힘의 평형을 이루며, 물질이 적으면 팽창하는 힘만 있어서 계속 팽창한다는 것이다. (참고로 위 내용의 결과는 나와 같은 시대 학교를 다닌 분에 한해서 고등학교 종합과학 파트에 나온다.)

​

Measurement of Our Universe Future

실제로 과학자들은 위 수치들을 측정하여 우리 우주의 미래를 점쳐보았다. 측정된 수치는 아래와 같다.

$H_0=67.66\pm 0.42\ \left[\frac{km}{s\cdot Mpc}\right]=\left(2.1927664\pm 0.0136\right)\times 10^{-8}s^{-1}$H0​=67.66±0.42 [kms·Mpc​]=(2.1927664±0.0136)×10−8s−1​

$\Lambda =1.1056\times 10^{-52}m^{-2}=4.33\times 10^{-66}eV^2=2.888\times 10^{-122}E_{plank}^2,\ \ E_{plank}\equiv \sqrt{\frac{\hbar c^5}{G}}$Λ=1.1056×10−52m−2=4.33×10−66eV2=2.888×10−122E2plank​, Eplank​≡√ℏc5G​​

$\Omega _{\Lambda }=\frac{c^2\Lambda }{3H^2}=0.6889\pm 0.0056$ΩΛ​=c2Λ3H2​=0.6889±0.0056​

$\rho _c=\frac{3H^2}{8\pi G}=8.5\times 10^{-27}\ \frac{kg}{m^3}$ρc​=3H28πG​=8.5×10−27 kgm3​​

$\Omega _m=\Omega _{baryon}+\Omega _{dark\ matter}=0.3111\pm 0.0056$Ωm​=Ωbaryon​+Ωdark matter​=0.3111±0.0056​

$\therefore \Omega =\ \Omega _m+\Omega _{\Lambda }=1\pm 0.0112$∴Ω= Ωm​+ΩΛ​=1±0.0112​

아쉽게도 측정 결과로는 아직 우리 우주의 미래를 점칠 수 없다. Ω가 1과 매우 근사하지만, 오차에 따라 작아질수도, 커질수도, 비슷해질 수도 있는 상황이다.

​

Cosmological Constant Effects

우주상수가 우주의 미치는 영향은 에너지 밀도 증가와 가속 팽창이다.

$H^2=\frac{8\pi G\rho }{3}+\frac{1}{3}c^2\Lambda -c^2\ \frac{k}{R^2}\left[\text{Friedmann Equation}\right]$H2=8πGρ3​+13​c2Λ−c2 kR2​[Friedmann Equation]​

$\ H^2=\frac{8\pi G}{3}\left(\rho +\frac{c^2\Lambda }{8\pi G}\right)-c^2\ \frac{k}{R^2}$ H2=8πG3​(ρ+c2Λ8πG​)−c2 kR2​​

$\rho _{new}\equiv \rho +\frac{c^2\Lambda }{8\pi G}$ρnew​≡ρ+c2Λ8πG​​

$\ H^2=\frac{8\pi G}{3}\rho _{new}-c^2\ \frac{k}{R^2}$ H2=8πG3​ρnew​−c2 kR2​​

$From\ R_{ij}-\frac{1}{2}g_{ij}=\frac{8\pi G}{c^4}T_{ij}-\Lambda g_{ij}$From Rij​−12​gij​=8πGc4​Tij​−Λgij​​

$q\equiv -\frac{\ddot{R}}{RH}.\ Then,$q≡− ¨R RH​. Then,​

$3qH^2=4\pi G\left(\rho +\frac{3P}{c^2}\right)-C^2\Lambda =4\pi G\left\{\rho +\frac{c^2\Lambda }{8\pi G}+\frac{3}{c^2}\left(P-\frac{c^4\Lambda }{8\pi G}\right)\right\}$3qH2=4πG(ρ+3Pc2​)−C2Λ=4πG{ρ+c2Λ8πG​+3c2​(P−c4Λ8πG​)}​

$=4\pi G\left(\rho _{new}+\frac{3}{c^2}P_{new}\right)$=4πG(ρnew​+3c2​Pnew​)​

$\rho _{new}\equiv \rho _m+\rho _{\Lambda }\ \ \ P_{new}\equiv P_m+P_{\Lambda }$ρnew​≡ρm​+ρΛ​ Pnew​≡Pm​+PΛ​​

$\rho _{\Lambda }=\frac{c^2\Lambda }{8\pi G}\ \ P_{\Lambda }=-\frac{c^4\Lambda }{8\pi G}$ρΛ​=c2Λ8πG​ PΛ​=−c4Λ8πG​​

(위 역시 아인슈타인 중력장 방정식에서 q를 어떻게 대입했는지에 대한 내용은 강의에 나오지 않았다.)

위 결과를 보면 우주상수는 에너지밀도를 늘리고, 압력 P는 감소하는 효과를 낸다. 즉, 음압(negetive pressure)를 낸다. 기존의 압력이 공간을 누르는 힘이면, 음압은 반대로 공간을 팽창시키는 힘을 낸다.

우주 상수 Λ는 에너지 밀도를 증가시키고, 우주를 팽창시키는 효과를 낸다.

우주 상수를 암흑에너지로 생각한다면, 암흑에너지의 효과도 우주를 팽창시키는 효과다.

​

여기서 이상기체 상태방정식처럼 압력이 밀도와 비례한다고 생각해보자.

$Let\ P=\omega \rho c^2\ \ \ \text{cf)}\ P=R\frac{N}{V}T=\frac{M}{V}\ \frac{RT}{m}=\rho \frac{RT}{m}$Let P=ωρc2 cf) P=RNV​T=MV​ RTm​=ρRTm​​

$3gH^2=\left(1+3\omega \right)4\pi G\rho _{new}$3gH2=(1+3ω)4πGρnew​​

만약 압력에 대한 비례상수 ω가 -1/3보다 작다면, 우항은 음수가 된다. 근데 q는 R의 시간 두번 미분이기에 우주의 팽창 가속력을 다룬다. q가 팽창 가속력에 음수이기에, 우항이 음수면 팽창 가속력은 양수이다. 즉, 우주가 가속팽창함을 나타낸다. (실제로 측정된 omega value 값은 찾지 못했다.)

​

Friedmann equation from Einstein field equation

https://youtu.be/cbRy3sXDJ-U

 

​

위 영상을 보면 프리드만-레메트르-로버트슨-워커 계량에서 Affine connection을 구하고, Affine connection으로부터 리만 곡률 텐서를 구한다. 리만 곡률 텐서에서 다시 리치 곡률 텐서와 스칼라 곡률을 구할 수 있다. 그리고 에너지-운동량 텐서에 대한 가정을 통해서 프리드만 방정식을 유도할 수 있다. 자세한 내용은 시간이 나면 나중에 수정해서 올려놓겠다.

[출처] [일반 상대성이론] 우주론 (cosmology); 우주의 미래와 가속 팽창|작성자 별세포